🤖Fine-tuning an LLM using Outcome Based Reward Function

Introduction

Before we learn how to fine-tune an LLM using Outcome Based Reward Function, let’s get the basics right. If you already have knowledge in LLM and fine-tuning, you can proceed to section Introducing MOTIF.

What is RLFT?

Reinforcement Learning Fine-tuning or RLFT, is a technique employed in fine-tuning a pre-trained LLM using Reinforcement Learning. Think of it like this - you’re a student taking Calculus. This math-heavy course requires knowledge of limits and derivatives, so you need prerequisites before enrolling.

Now let’s say you completed the prerequisite course. However, you’ve either forgotten some tricks or important rules after the course ended. But these are quite necessary for your upcoming calculus class.

Here’s the question: Do you re-take the “Limits and Derivatives” class or revise using your notes and cheatsheets? You go for the latter because it’s efficient. That’s fine-tuning in a nutshell. LLMs are pre-trained over massive datasets, but this doesn’t guarantee they’re ready for specific real-world problems. Hence, fine-tuning adjusts their responses for particular tasks or styles.

Fine-tuning can be achieved through either Supervised Fine-tuning (SFT) or RLFT. RLFT gained popularity after the introduction of Group Relative Policy Optimization (GRPO) by researchers at Deepseek Lab.

What is GRPO?

Group Relative Policy Optimization or GRPO is an RLFT technique that relatively ranks responses from samples generated by an LLM during fine-tuning to enhance its reasoning capability.

Picture this: You’re now the Calculus teacher with 30 students. During class, instead of calling on one student for an answer, imagine you ask a question and four students raise their hands. Each gives their response, and now you rank them - the best response gets praised while the worst gets constructive feedback (though in GRPO, we simply penalize it).

GRPO samples $m$ responses, calculates a reward for each response, and updates the model to make high-reward responses more likely in the future.

Introducing MOTIF

We’ve seen GRPO - but what if all the initial answers are wrong, yet one response has the potential to reach the correct answer if allowed to develop further? This is where MOTIF shines.

MOTIF builds on vanilla-GRPO by sampling $m$ responses, but adds a new layer called “Outcome-Based” reward function. Rather than ranking answers from their first attempt, MOTIF lets the LLM continue reasoning through $k$ trajectories to see where each initial response leads.

What’s Different from Vanilla-GRPO?

While vanilla-GRPO directly ranks first responses, MOTIF evaluates responses based on their downstream potential. This creates richer training signals and achieves the same performance with 85% fewer samples (using only 15% of the data) - as seen in the research.

MOTIF incorporated into the GRPO pipeline

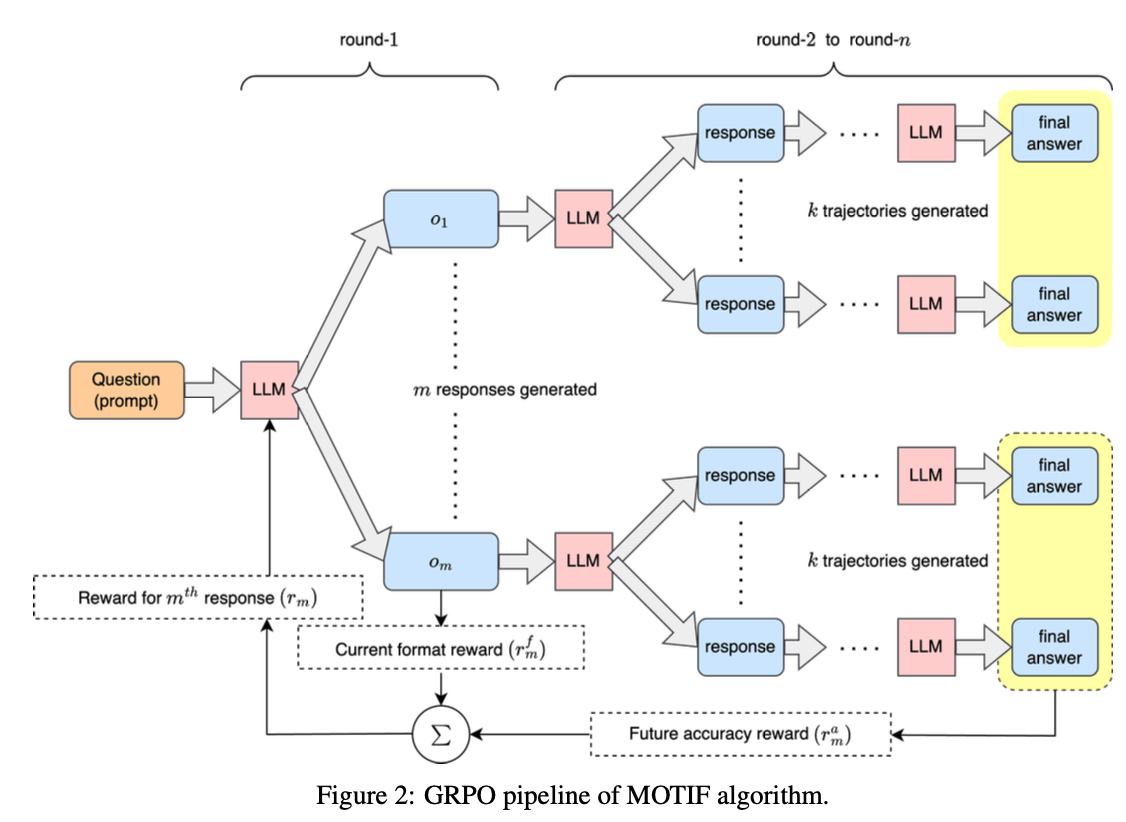
How Does It Work?

Imagine the LLM trying to solve for the math problem: “What is 15 × 24?”

MOTIF algorithm

The Process:

1. Generate First-Round Responses (with temperature $t=0.8$ for diversity):

   • Response 1: Suppose it says - “I’ll start by calculating 15 × 20 = 300…”
   • Response 2: Likewise - “I’ll use 15 × 25 = 375 as a reference point…”

2. Run Multiple Trajectories: For each first-round response, generate $k$ complete solutions:

   • From Response 1: After 2 trajectories, one gets 360 ✓ and the other gets 340 ✗
   • From Response 2: After 2 trajectories, both get 360 ✓✓

3. Calculate Rewards:

   • Format reward $r^f_i$: Check if response uses correct tags (1 if yes, 0 if no)
   • Accuracy reward $r^a_i$: Fraction of trajectories reaching correct answer.
   • Total reward: $r_i = r^f_i + r^a_i$

For our example:

• Response 1: $r_1 = 1 + 0.3 = 1.3$ (correct format + 30% success rate)
• Response 2: $r_2 = 1 + 1.0 = 2.0$ (correct format + 100% success rate)

4. Update Model: GRPO sees Response 2 scored higher, so it updates the policy to make similar starting approaches more likely.

The mathematical formulation:

1. First-round format check:

   $$r^{f}_{i} = \mathbb{I}(\text{correct tags in } o_{i})$$

2. Accuracy across trajectories:

   $$r^{a}_{i} = \frac{1}{k}\sum^{k}_{j=1}\mathbb{I}(\text{correct answer in } f^{i}_{j})$$

3. Total reward:

   $$r_{i} = r^{f}_{i} + r^{a}_{i}$$

Why Does MOTIF Outperform Vanilla-GRPO?

Three key advantages emerge from the research:

1. Richer Gradient Signals: Instead of binary feedback (right/wrong), MOTIF provides probabilistic signals (like 0%, 25%, 50%, 75%, 100% success rates with $k$ trajectories).

2. Noise Reduction: Averaging reward over multiple trajectories reduces variance - a good approach might occasionally fail, but multiple trials reveal its true quality.

3. Implicit Curriculum Learning: The model learns where-in intermediate reasoning patterns lead to success without explicit supervision on what “good reasoning” looks like.

Experimentation

The experiments used an NVIDIA A100 GPU (40GB) with LoRA adapters (rank $r=64$) to fine-tune Qwen2.5-3B-Instruct using parameter-efficient fine-tuning. Training used the GSM8K dataset.

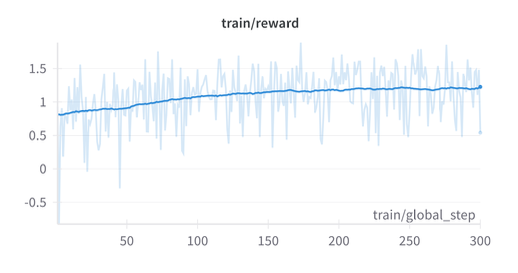
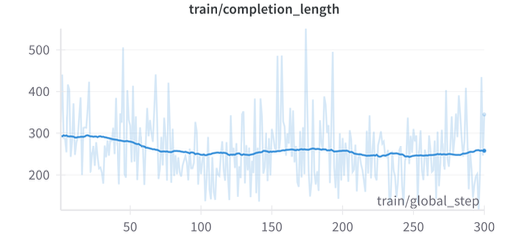
Key comparison : Vanilla-GRPO used 2000 samples while MOTIF used only 300 samples (15%), yet achieved better results. See the pre-print for detailed prompts.

Results

For pass@1 accuracy, MOTIF shows 3.8% and 3.3% improvements over vanilla GRPO on MATH500 and AIME2024 benchmarks respectively, while using only 15% of training samples.

Performance comparison: MOTIF vs vanilla GRPO

The training dynamics reveal interesting patterns:

MOTIF's reward grows smoothly from the start, unlike vanilla GRPO's delayed improvement

MOTIF's responses become more concise as reasoning distributes across rounds

Applications

MOTIF looks promising for domains with scarce labeled data. Consider circuit design generation - with limited training data due to IP restrictions, MOTIF’s sample efficiency could enable effective fine-tuning where traditional approaches fail.

Acknowledgment

All content and images are for educational purposes. Credits to authors Purbesh Mitra and Sennur Ulukus from the University of Maryland for developing this novel RLFT technique.